CultureMath
Ressources adaptées au programme de mathématiques de seconde
Le programme du cycle 4 (5e, 4e, 3e ; rentrée 2016) est disponible en version pdf.
Il est découpé en quatre grands thèmes, et assorti de l'enseignement de l'informatique et des EPI. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
- Nombres et calculs ;
- Organisation et gestion de données, fonctions ;
- Grandeurs et mesures ;
- Espace et géométrie
- Enseignement de l'informatique
- EPI (Enseignements pratiques interdisciplinaires)
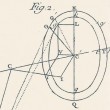
Bien qu'elle fut découverte par l'astronome grec Hipparque au IIème siècle av. J.C., il a fallu attendre la fin du XVIIème siècle pour qu'une explication soit donnée par Newton du mouvement de la précession des équinoxes, qui consiste en un déplacement de l'axe de rotation de la terre dans l'espace selon un cône dans une période de 26 000 ans. En 1748 D'Alembert s'attaque lui aussi avec une très grande motivation au sujet. Il publie dès l'année suivante ses "Recherches sur la précession des équinoxes & sur la nutation de l'axe de la Terre dans le système Newtonien". Dans cet ouvrage d'astronomie théorique, D'Alembert tout en reconnaissant le génie de Newton souligne les imperfections de ses calculs, et établit pour la première fois une théorie très précise et exacte non seulement du mouvement de précession mais aussi de la petite boucle de nutation découverte deux ans auparavant par Bradley...
Extrait d'une lettre de D'Alembert à Euler du 20 juillet 1749 sur le problème de l'apogée : "Quoiqu'il en soit, Monsieur, je vous avoüeray, qu'en supposant même que nous ne nous soyons point trompés dans le calcul du mouvement de l'apogée, je ne goute nullement l'opinion où vous paroissés être, et où M. Cairaut etoit aussy, que l'attraction ne suit pas exactement la loy inverse du quarré des distances."
Une raison pour laquelle la mathématique jouit d’une estime particulière, au-delà de toutes les autres sciences, est que ses lois sont absolument certaines et incontestables, quand celles des autres sciences sont dans une certaine mesure discutables et en danger permanent d’être renversées par des faits nouvellement découverts. »
Les trois sœurs Mina a deux fois l’âge qu’avait Tina lorsque Anna avait l’âge de Mina. Lorsque Mina aura l’âge d’Anna, l’âge de Tina sera le triple de l’âge qu’avait Anna lorsque Anna avait l’âge de Mina. Lorsque la plus jeune aura triplé son âge, les deux autres auront ensemble 160 ans. Quel âge a aujourd’hui chacune des trois sœurs ?
Les mathématiques ont une image froide et monolithique.L’enseignement y est pour quelque chose, tant on apprend à l’école des suites de théorèmes et de démonstrations désincarnés. Pourtant, « un mathématicien n’est pas une machine à déduire, mais un être humain. »...
Ce livre est un recueil d'exercices corrigés tirés de situations de la vie courante, concernant essentiellement les dépenses, mais aussi les économies d'énergie, la pollution, la santé. Le principe est de partir d'un problème réel, et chercher dans les programmes de collège les outils pour le résoudre. Les auteurs enseignent respectivement en collège, université et lycée ; ils sont membres de l'IREM de Basse Normandie.
À quoi sert la clef du n° de sécurité sociale ? Quels sont les tracés qu’on peut faire sans lever le crayon ? Qu’y a-t-il au centre d’un carré magique ? Platon et Euler, inventeurs du ballon de football ? Comment marche l’algorithme d’ordre des résultats dans un moteur de recherche ? Pourquoi y a-t-il une station de RER Laplace ? Comment fonctionne un détecteur d’incendie dans un hôtel ? Pourquoi la Terre perd-elle le Nord ?
ssu de travaux effectués au sein de l’IREM de Franche‐Comté, le présent ouvrage exploite et analyse «Solutions peu connues de différens (sic) problèmes de géométrie » que F. J. Servois publia en 1805.
Nous étudions, dans son contexte historique et mathématique, le cours de géométrie du franc-comtois F.-J. SERVOIS qui fut prêtre, lieutenant d'artillerie puis professeur en école d'artillerie.
Cycle de conférences organisées depuis 2006 par la Bibliothèque nationale de France et la Société mathématique de France.
Mêlant histoire et mathématiques, ces conférences permettent à un large public de découvrir les mathématiques contemporaines.
Le principe: le conférencier choisit un texte mathématique datant de plusieurs dizaines d’années, voire bien plus, qui l’a particulièrement influencé...