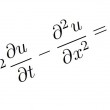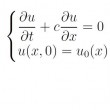CultureMath
Neighborhood filters are image and movie filters which reduce the noise by averaging similar pixels. The object of the paper is to present a unified theory of these filters and reliable criteria to compare them to other classes of filters.
Le bruit sonore est de plus en plus considéré comme une nuisance intolérable, mais qu'en est-il du bruit visuel ? Toutes les images et les films digitaux comportent un bruit, qui gêne la vision et impose des contraintes technologiques de prix, de taille et d'énergie aux caméras. Des progrès récents dans la compréhension de la structure des images permettent d'éliminer le bruit des images et des films sans les endommager.
Le bruit sonore est de plus en plus considéré comme une nuisance intolérable, mais qu'en est-il du bruit visuel? Toutes les images et les films digitaux comportent un bruit, qui gêne la vision et impose des contraintes technologiques de prix, de taille et d'énergie aux caméras. Des progrès récents dans la compréhension de la structure des images permettent d'éliminer le bruit des images et des films sans les abimer.
Le bruit sonore est de plus en plus considéré comme une nuisance intolérable, mais qu'en est-il du bruit visuel ? Toutes les images et les films digitaux comportent un bruit, qui gêne la vision et impose des contraintes technologiques de prix, de taille et d'énergie aux caméras. Des progrès récents dans la compréhension de la structure des images permettent d'éliminer le bruit des images et des films sans les abimer.
Du compact-disc, au DVD, en passant par l'appareil photo numérique, le scanner, et une hypothétique télévision numérique (plus en panne politique que technologique), le numérique a fait une entrée progressive mais écrasante et sans doute irréversible dans la vie quotidienne. Ce n'est évidemment pas sans raison : pour le meilleur et pour le pire, les signaux numériques sont plus simple à dupliquer (et donc à diffuser), ils peuvent être efficacement compressés et transmis, ils sont faciles à stocker, et on peut aisément les manipuler.
Peut-on calculer l'intégrale d'une fonction (sur l'intervalle [0,1] par exemple) si l'on ne connaît que sa valeur en 3 points ? Évidemment non, sauf si l'on sait en outre qu'il s'agit d'un polynôme de degré 2 ! Facile, me direz vous : dans ce cas, la donné des valeurs en trois points, quels qu'il soient, permet de retrouver le polynôme et donc de calculer cette intégrale. Beaucoup plus fort : si l'on choisit correctement ces trois points, on peut calculer l'intégrale de n'importe quel polynôme de degré 5, en ne connaissant que sa valeur en nos trois points. Et cette fois, plus question de trouver le polynôme.
L'équation de la chaleur est à l'origine de nombreux problèmes, souvent difficiles, et a fait couler beaucoup d'encre. Nous nous restreignons ici à un cas particulier, avec des conditions de départs assez simple, de sorte que la solution exacte soit connue. Celle-ci va nous permettre d'apprécier l'efficacité (ou les défauts) des méthode numériques de résolution approchée.
La simulation numérique de l'équation de la chaleur pose parfois quelques problèmes, et pas seulement de capacité de calcul. Nous allons voir en effet que tous les algorithmes ne sont pas équivalents, loin de là...
La simulation numérique ne pose pas toujours seulement des problèmes de capacités de calcul : même avec des ordinateurs de plus en plus puissants, l'opération laisse encore des problèmes au mathématicien ! Il s'agit en effet de mettre en place des algorithmes qui fonctionnent, et nous allons voir que, même dans des cas très simples, on ne peut pas faire n'importe quoi.