CultureMath
Ressources adaptées au programme de mathématiques de première S
Le programme des premières S (B.O. 2010) est disponible en version pdf.
Il est découpé en trois grands thèmes, et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
Deux capacités transversales :
Né en 1973 à Paris, Fabien Napolitano est directeur général du site Brestois de la société Ixsea, leader mondial dans le domaine des systèmes de positionnement pour les bateaux et sous-marins. Pourtant il n'a pas fait d'études d'ingénierie, mais est titulaire d'un doctorat en mathématiques pures, et a fait des aller-retours entre le monde de la recherche fondamentale et celui de l'industrie.
Ce texte a une forme inhabituelle sur ce site : c'est un problème destiné à explorer certaines propriétés de l'hyperbole y = 1/x. Il mélange géométrie plane, géométrie analytique et utilisation des moyens de calcul modernes, et pourra donner des idées d'exercices aux professeurs... tout en leur pemettant de s'exercer !
C. F. Gauss est toujours considéré par certains comme le plus grand mathématicien de tous les temps. Sa capacité calculatoire hors du commun, couplée à son goût pour la contemplation des idées abstraites l'on amené à résoudre des problèmes (parfois vieux de millénaires !) et à envisager avec une clarté géniale (bien qu'inquiète) les idées qui feraient les mathématiques du futur.
Dans un article de 1950, devenu justement célèbre, Alan Turing propose, en vue d'opérer une comparaison fonctionnelle entre le cerveau et la machine, un jeu qu'il appelle "jeu de l'imitation". Cet article fut un pas décisif dans le domaine de la philosophie de la connaissance.
Le texte que nous vous proposons présente un point de vue cognitif sur la question de la différence entre la pensée humaine, continue, et le fonctionnement d'une machine à états discrets.
Une équation n'est rien d'autre qu'une égalité entre deux membres. Souvent, il s'agit de déterminer une certaine quantité, connaissant simplement une égalité qui fait intervenir cette quantité inconnue. On parle d'équation algébrique lorsque l'on cherche à déterminer les racines d'un polynôme. Nous allons ici nous intéresser plus spécifiquement à ce type d'équation, et voir notamment des méthodes générales pour résoudre les équations algébriques de degré allant de 1 à 4.
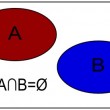
La théorie des ensembles est entre autres choses une tentative de formalisation, dans un système d'axiomes assez simples et si possible intuitifs, de l'ensemble des connaissances mathématiques. En particulier, l'essentiel de l'arithmétique ou de l'analyse se déduirait de façon élémentaire, quoique assez longue, de cette axiomatique.
Comment empiler efficacement des oranges (ou tout autre fruit sphérique) de façon à obtenir un tas occupant aussi peu de volume que possible ? Est-il préférable d'empiler des couches où les fruits sont disposés en carrés, ou une disposition en triangles est-elle plus efficace ?
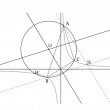
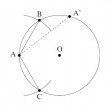
Étant donné un cercle, si l'on trace une corde au hasard sur ce cercle, quelle est la probabilité pour que celle-ci soit plus longue que le rayon du cercle ? Cette question, connue sous le nom de "paradoxe" de la corde de Bertrand, est particulièrement judicieuse pour illustrer la notion de mesure de probabilité. Nous allons voir que la réponse varie en fonction du mode de construction, chaque façon de penser étant lié à une mesure particulière.