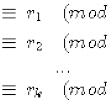CultureMath
Ressources adaptées au programme de mathématiques de première ES/L
Le programme commun des premières ES et L (B.O. 2010) est disponible en version pdf.
Il est découpé en deux grands thèmes, et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
Deux capacités transversales :
D'Alembert a signé environ 1700 articles, dont 90 % d'articles scientifiques parmi lesquels 90 % concernent les mathématiques au sens large, c'est-à-dire comprenant la mécanique, l'hydrodynamique, l'acoustique, l'astronomie, l'optique. C'est à ces derniers qu'est consacré ce chapitre.
Voici une séquence de travail scénarisée autour d’un texte proposant un algorithme qui permet de résoudre un système de trois congruences simultanées modulo des entiers premiers entre eux deux à deux.
Dans ce chapitre nous avons sélectionné deux types de sources. D’une part, des énoncés choisis pour leur présentation imagée du problème : sous un habillage « concret », ces textes nous montrent entre autres l’imagination au service des mathématiques. C’est ce qui a motivé leur regroupement et non les mathématiques mises en œuvre pour la résolution. Certaines solutions sont « brutes », d’autres sont accompagnées de commentaires, d’explications, ou de véritable justification mathématique.
Découvrez ou redécouvrez les grandes idées qui font la force des mathématiques en suivant l'incroyable destinée de la question de Kakeya. Ou comment une devinette apparemment enfantine a pu croître et se ramifier jusqu'à se transformer en un véritable défi lancé aux plus grands cerveaux de notre temps ?
Dans cette conférence destinée aux collégiens et aux lycéens, Cédric Villani nous fait suivre un long fil qui part de la géométrie du plan euclidien, en passant par la théorie des nombres, la topologie, la géométrie fractale, pour nous mener à ses travaux en théorie cinétique des gaz. Il nous montre alors comment cette théorie lui a permis de revenir à la géométrie, non euclidienne cette fois-ci !
Brescia, février 1512. Les armées françaises de Louis XII envahissent la ville, la pillent et massacrent ses habitants. Dans la fureur du combat, un garçon de douze ans est frappé d’un coup de sabre en plein visage. Grièvement blessé, il restera bègue toute sa vie et sera connu sous le nom de Tartaglia (« bègue » en italien)...
Nous étudions, dans ce chapitre, la résolution d’un système de deux congruences simultanées, les modules étant premiers entre eux, telle qu’elle serait menée au lycée. Même si nous nous appuyons sur un problème historique, nous employons les notations modernes, notamment le signe de congruence introduit par Gauss...
Le 31 mai 1832, le mathématicien Évariste Galois est âgé de 21 ans ; il meurt en duel pour les yeux de sa belle. La veille, il a résumé ses travaux. Ainsi s’achève ce destin singulier. Ardent républicain, il est chassé de l'École normale pour ses discours politiques. Il prend d’autres prises de position violentes, et est incarcéré à 20 ans pour avoir porté un toast à la mort du roi Louis-Philippe...
Issus du séminaire d'épistémologie de l'IREM (Univ. Paris 7) et d'un colloque de philosophie des mathématiques, dirigés par Michel Serfati, ces articles décrivent les compas de Descartes, une méthode de résolution par géométrisation, la place de la psychologie chez Boole, Cantor et Brouwer, les machines de Turing, les lignes de courbure d'une surface mises à jour par Monge, le rapport contenu du travail du mathématicien...
Vous n’arrivez pas à convaincre vos proches que vous faites des mathématiques sous prétexte que c’est un art, la clé du monde, la beauté à l’état pur, que la philosophie n’est pas assez exacte ou que tout le monde a essayé de vous dissuader ?