CultureMath
Question du jeudi #56 : Montrer que pour tout $n > 1$, le nombre $n^4 + 4$ n'est pas premier.
Question du jeudi #48 : Lors d'un tournoi de Quidditch, quatre équipes s'affrontent une fois chacune. Il est alors possible de lister les équipes, de telle sorte que chacune ait battu la suivante : par exemple, Gryffondor a battu Poufsouffle, qui a battu Serdaigle, qui a battu Serpentard.
Est-il toujours possible de faire une telle liste ? Quid si le tournoi voit s'affronter plus de quatre équipes ? On supposera dans cette question qu'un match de Quidditch ne peut pas être nul.
Question du jeudi #46 : Roger est un joueur de tennis de très haut niveau, Éric un joueur du dimanche. On vous propose de jouer trois parties contre les deux, alternativement, et de vous donner un prix si vous gagnez deux parties consécutives. Avez-vous intérêt à jouer Roger, Éric puis Roger, ou Éric, Roger puis Éric ?
Question du jeudi #44 : Un véhicule parcourt une route de 100 kilomètres. Son GPS estime le temps restant à parcourir en supposant que la vitesse moyenne sur le trajet restant sera égale à la vitesse moyenne depuis le départ. Au bout de 40 minutes, le GPS indique qu'il reste une heure de trajet. Est-il possible que le GPS donne la même indication pendant les cinq heures suivantes ? Si oui, combien de kilomètres resteront-ils à parcourir au bout de ces cinq heures ?
On voit facilement qu'il est possible de recouvrir un carré par quatre triangles équilatéraux de même côté. Est-il possible de n'en utiliser que trois ?
Question du jeudi #41 : Combien de nombres à 6 chiffres sont multiples de 164 et se terminent par 164 ?
Version française d'une initiative mexicaine, le Calendrier Mathématique vous propose une énigme mathématique à résoudre tous les jours de la semaine. Celles-ci peuvent être de nature arithmétique, géométrique, ou faire simplement appel à un raisonnement ingénieux.
Auteur : Jean-Yves Labouche, École franco-américaine du Puget Sound (Mercer Island, Washington, États-Unis)
Mots-clefs : Construction géométrique, Pavage, Hexagone, Travail collectif
Description des étapes menant les élèves d’une classe de 6e à la réalisation d’un pavage hexagonal de très grandes dimensions en dehors de la classe et avec des outils peu ordinaires pour un exercice de géométrie.
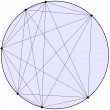
Question du jeudi #39 : On place n points sur un cercle et l'on trace toutes les cordes reliant ces deux points. On suppose en outre que les cordes sont en position générale, c'est-à-dire que trois cordes ne sont jamais concourantes. Combien de points d'intersection y aura-t-il à l'intérieur du disque ?
Question du jeudi #38 : Alice et Bob jouent à un jeu~: 38 pièces, de diverses valeurs, sont alignées sur une table en face d'eux. Alice choisit une des deux pièces qui occupent une extrémité de la rangée et l'empoche. Bob fait de même, et ainsi de suite jusqu'à ce que Bob empoche la trente-huitième pièce. Montrer qu'Alice peut être sure d'empocher au moins autant d'argent que Bob.