CultureMath
Ressources adaptées au programme de mathématiques de terminale S
Le programme des premières S (B.O. 2011) est disponible en version pdf.
Il est découpé en trois grands thèmes (plus deux pour l'enseignement de spécialité), et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
- Analyse
- Géométrie
- Statistique et probabilités
- Arithmétique (enseignement de spécialité)
- Matrices et suites (enseignement de spécialité)
Deux capacités transversales :
Institution des Jeux Olympiques, 776- Fondation des premières "colonies" occidentales, vers 750- Débuts de l'urbanisme fonctionnel...
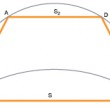
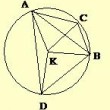
Dans la construction de ses trois lunules Hippocrate combine le principe (H) avec des relations métriques simples pour en déduire des égalités entre segments de cercles...
Ce livre est le produit de la préparation de l'équipe d'Allemagne aux Olympiades internationales de mathématiques tout au long des quelques trente ans où Arthur Engel a joué un rôle majeur dans cette préparation...
Apollonius de Perge, Les Coniques. Trad. franç. P. ver Eecke. Paris, Blanchard 1963.
Archimède,Œuvres (inclut les commentaires d'Eutocius d'Ascalon). Ed. et trad. franç. Ch. Mugler, 4 vol., Paris, Belles-Lettres, 1970-74...
Aristarque de Samos, Autolycos de Pitane, Euclide, Archimède de Syracuse...
Un segment de cercle est la figure mixtiligne découpée par une sécante dans un cercle...
Aucun texte géométrique antérieur aux Éléments d’Euclide (IIIe s. avant notre ère) ne nous est parvenu. Pour les mathématiques des époques archaïque et classique (VIe-IVe s.), nous devons nous contenter de témoignages et de quelques fragments. Le dossier le moins mal documenté concerne Hippocrate de Chio (deuxième moitié du Ve s.). Son activité, contemporaine de celle de son célébrissime homonyme, le médecin Hippocrate (de Cos), correspond à l’âge d’or de la Grèce des cités, à la mise en place des institutions démocratiques, au développement de nouveaux moyens de communication et de « publication » (au sens premier de « rendre public »), notamment l’apparition d’une littérature technique en prose qui coïncide avec des formes rudimentaires de « spécialisation » : histoire, philosophie, mathématiques … Dans la cité d’Athènes — la moins mal connue —, dès le début du IVe s. avant notre ère, un débat divise les spécialistes de l’éducation sur la place qu’il faut accorder à la géométrie.
Bien des approches de la géométrie grecque ancienne sont possibles. Les grands textes des auteurs hellénistiques, notamment certains fameux problèmes tels que la quadrature du cercle ou la duplication du cube, ont joué un rôle indéniable dans l’histoire des mathématiques jusqu’à une date récente et ont intéressé — et intéressent toujours — les historiens des sciences, les enseignants, le public cultivé … Plusieurs questions restent cependant sans réponse : les premières recherches mathématiques des Grecs nous échappent en grande partie ; nous ignorons à peu près tout de la biographie (en particulier intellectuelle) des principaux géomètres ; les modalités de l’enseignement des mathématiques dans l’Antiquité nous sont fort mal connues. Bien que lacunaires, les sources ne sont pourtant pas muettes. Des oeuvres mathématiques majeures sont parvenues jusqu'à nous au terme de processus de transmission complexes, en particulier par le biais de la tradition savante écrite en langue arabe. Dans ce dossier, Bernard Vitrac présente les oeuvres d'Hippocrate, Euclide, Archimède, Apollonius, Ptolémée, Héron, Ménélaos..., et évoque des lieux et des contextes historiques particulièrement importants pour l'histoire des mathématiques (les cités ioniennes, Athènes, Alexandrie...). Le dossier se répartit en dix articles, complétés par des outils annexes qui seront utiles aux enseignants : bibliographie, chronologie, carte, ainsi qu'une liste des oeuvres mathématiques grecques parvenues jusqu'à nous.
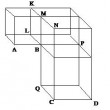
Quand on a quatre droites continûment proportionnelles AB, CD, EF, GH (AB : CD :: CD : EF :: EF : GH), les Anciens disent que le rapport AB : GH est le rapport triplé du rapport AB : CD. Ce que nous écririons, en termes modernes..
Strepsiade encourage son fils à étudier avec Socrate pour être moins dépensier. Celui-ci refuse. Strepsiade, quoique très âgé, décide de se faire instruire lui-même. Il se présente au « pensoir » de Socrate et frappe à la porte...