CultureMath
Ressources adaptées au programme de mathématiques de terminale S
Le programme des premières S (B.O. 2011) est disponible en version pdf.
Il est découpé en trois grands thèmes (plus deux pour l'enseignement de spécialité), et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
- Analyse
- Géométrie
- Statistique et probabilités
- Arithmétique (enseignement de spécialité)
- Matrices et suites (enseignement de spécialité)
Deux capacités transversales :
Ce chapitre revient sur le cas « Hippocrate », cette fois du point de vue des techniques géométriques. La tradition ancienne attribue, à tort ou à raison, trois contributions majeures au géomètre de Chio, lesquelles esquissent les principales articulations à venir de la géométrie grecque :
- Il aurait été le premier à rédiger des Éléments de géométrie.
- Il aurait introduit la procédure de réduction d’un problème — en l’occurrence celui de la duplication du cube — à un autre, celui de l’insertion de deux moyennes proportionnelles entre deux segments de droite (problème paradigmatique de la géométrie dite ultérieurement « solide »).
- Enfin son nom est attaché à la quadrature de certaines portions de cercle (appelées « lunules »), possiblement mobilisées pour une tentative de résolution du célébrissime problème de la quadrature du cercle.
Cette contribution nous est connue grâce à un précieux témoignage d’Eudème de Rhodes (IVe s. avant notre ère) — historien de la géométrie et disciple d’Aristote — transmis par le commentateur Simplicius (VIe s.). On y rencontre un style géométrique localement déductif, utilisant des diagrammes, déjà assez proche de celui que l’on trouvera chez Euclide.
La conservation de ce témoignage ne relève par du pur hasard : le Maître (i.e. Aristote) avait parlé d’Hippocrate et sa tentative de quadrature fut tôt interprétée comme un paralogisme. Le premier géomètre grec tant soit peu connu de nous était-il un filou ?
Abel était, contrairement à Galois, un homme affable. Il aimait, outre nos chères mathématiques, la vie, les femmes, les voyages, bref l’aventure sous toutes ses formes. Il en a profité au maximum, au cours de sa courte vie pleine d’aléas tant familiaux que physiques. Il est banal de dire que, malgré l’aridité de leurs études, les mathématiciens sont des hommes (ou des femmes) comme les autres qui aiment et qui souffrent.
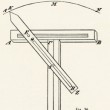
Mesurer les surfaces avec des instruments, pour lycéens (terminales), étudiants, enseignants et tout public curieux. Marie-José Durand-Richard présentera les instruments graphiques d’intégration utilisés en Europe au XIXe siècle en s’appuyant sur des documents réalisés à l’occasion de l’exposition du CNAM « Venez prendre l’aire! ».
Voici Images des Mathématiques 2006. Ce numéro rassemble des articles dont l’ambition est de faire connaître, de manière précise et attrayante, des mathématiques en train de se faire, à des lecteurs scientifiques, en particulier des étudiants en mathématiques...
Vous pensez sans doute que le voyage temporel appartient à la science-fiction. Détrompez- vous ! Depuis la théorie de la relativité d’Albert Einstein, nous savons que le temps est élastique, et les physiciens étudient aujourd’hui très sérieusement la possibilité de construire une machine à explorer le temps. Mais est-ce vraiment possible ?
La vie d’un homme savant et studieux est ordinairement étrangère au monde, et n’offre pas des incidens piquans par leur variété. Il est rare qu’elle ait quelque influence sur les événemens dont on est le plus occupé, plus rare encore qu’elle fixe la curiosité par des actions d’éclat. Car quoique la pensée tende à élever l’âme et à perfectionner le coeur ; le goût de la retraite, qui en est la suite, couvre d’une sorte d’obscurité les actions de ceux qui s’y livrent...
‘Les écritures mayas du nombre’ sont une synthèse des plus récents résultats d’analyses épigraphiques et linguistiques du corpus des écritures numérales et numériques réalisées par les scribes mayas depuis l’époque préclassique jusqu’à celle de la conquête espagnole. Interprétées dans le cadre des numérations parlées (de types protractif et additif) et dans celui des mesures de temps, la grande diversité des données analysées conduit à une typologie de l’ensemble des formes (notamment des zéros) et des systèmes mayas d’écriture du nombre, tant dans la représentation des dates et des petites durées, que dans celle des translations temporelles et des grandes durées.
Il s'agit d'un surprenant problème de collision qui a fait l'objet du "problème du mois" d'avril 2007: se présentant comme de la mécanique, il se révèle être un moyen (peu efficace!) de calculer Pi. La solution peut être obtenue par des méthodes géométriques ou algébriques.
En 79 diapositives commentées, ce document retrace l'histoire de la géométrie depuis ses origines mésopotamienne, égyptienne et grecque jusqu'aux théories non euclidiennes élaborées au XIXe siècle. Une première partie traite de l'élaboration de la géométrie comme science mathématique, une deuxième partie aborde les géométries non euclidiennes et introduit à une nouvelle conception de la géométrie. Plus qu'une simple histoire, il s'agit d'une réflexion épistémologique sur le rapport entre mathématique et réalité, qui intéressera aussi bien les philosophes que les mathématiciens.
Ce diaporama a été élaboré en Terminale scientifique à la demande conjointe d’Élisabeth ARBOGAST, professeur de mathématiques et Nafissa HAIDAR, professeur de philosophie, toutes deux au lycée Ribeaupierre de Ribeauvillé (Haut-Rhin). Au départ, Mme Haidar avait souhaité un exposé sur la géométrie non euclidienne et à partir de là, aborder les questions d’épistémologie au programme de la classe de Terminale Scientifique. Très vite, nous nous sommes mis d’accord sur l’objectif suivant : mettre en mouvement une dynamique de réflexion qui rompe avec le cloisonnement disciplinaire, et qui amène les élèves à se dire lorsqu’ils font des mathématiques : quel est le sens de ce que je fais en mathématiques ? En quoi est-ce une science exacte ? Comment s’est–elle construite ? Quel lien avec ce que je fais en philosophie ? Et lorsqu’ils sont en cours de philosophie : quels exemples puis-je tirer de mes autres apprentissages, mathématiques, physique, SVT, etc. pour donner corps aux concepts philosophiques, pour illustrer des thèmes comme intuition, évidence, vérité, rigueur, imagination, réalité ?