CultureMath
Ressources adaptées au programme de mathématiques de seconde
Le programme du cycle 4 (5e, 4e, 3e ; rentrée 2016) est disponible en version pdf.
Il est découpé en quatre grands thèmes, et assorti de l'enseignement de l'informatique et des EPI. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
- Nombres et calculs ;
- Organisation et gestion de données, fonctions ;
- Grandeurs et mesures ;
- Espace et géométrie
- Enseignement de l'informatique
- EPI (Enseignements pratiques interdisciplinaires)
Aucun texte géométrique antérieur aux Éléments d’Euclide (IIIe s. avant notre ère) ne nous est parvenu. Pour les mathématiques des époques archaïque et classique (VIe-IVe s.), nous devons nous contenter de témoignages et de quelques fragments. Le dossier le moins mal documenté concerne Hippocrate de Chio (deuxième moitié du Ve s.). Son activité, contemporaine de celle de son célébrissime homonyme, le médecin Hippocrate (de Cos), correspond à l’âge d’or de la Grèce des cités, à la mise en place des institutions démocratiques, au développement de nouveaux moyens de communication et de « publication » (au sens premier de « rendre public »), notamment l’apparition d’une littérature technique en prose qui coïncide avec des formes rudimentaires de « spécialisation » : histoire, philosophie, mathématiques … Dans la cité d’Athènes — la moins mal connue —, dès le début du IVe s. avant notre ère, un débat divise les spécialistes de l’éducation sur la place qu’il faut accorder à la géométrie.
Bien des approches de la géométrie grecque ancienne sont possibles. Les grands textes des auteurs hellénistiques, notamment certains fameux problèmes tels que la quadrature du cercle ou la duplication du cube, ont joué un rôle indéniable dans l’histoire des mathématiques jusqu’à une date récente et ont intéressé — et intéressent toujours — les historiens des sciences, les enseignants, le public cultivé … Plusieurs questions restent cependant sans réponse : les premières recherches mathématiques des Grecs nous échappent en grande partie ; nous ignorons à peu près tout de la biographie (en particulier intellectuelle) des principaux géomètres ; les modalités de l’enseignement des mathématiques dans l’Antiquité nous sont fort mal connues. Bien que lacunaires, les sources ne sont pourtant pas muettes. Des oeuvres mathématiques majeures sont parvenues jusqu'à nous au terme de processus de transmission complexes, en particulier par le biais de la tradition savante écrite en langue arabe. Dans ce dossier, Bernard Vitrac présente les oeuvres d'Hippocrate, Euclide, Archimède, Apollonius, Ptolémée, Héron, Ménélaos..., et évoque des lieux et des contextes historiques particulièrement importants pour l'histoire des mathématiques (les cités ioniennes, Athènes, Alexandrie...). Le dossier se répartit en dix articles, complétés par des outils annexes qui seront utiles aux enseignants : bibliographie, chronologie, carte, ainsi qu'une liste des oeuvres mathématiques grecques parvenues jusqu'à nous.
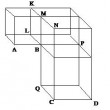
Quand on a quatre droites continûment proportionnelles AB, CD, EF, GH (AB : CD :: CD : EF :: EF : GH), les Anciens disent que le rapport AB : GH est le rapport triplé du rapport AB : CD. Ce que nous écririons, en termes modernes..
Strepsiade encourage son fils à étudier avec Socrate pour être moins dépensier. Celui-ci refuse. Strepsiade, quoique très âgé, décide de se faire instruire lui-même. Il se présente au « pensoir » de Socrate et frappe à la porte...
Ce chapitre revient sur le cas « Hippocrate », cette fois du point de vue des techniques géométriques. La tradition ancienne attribue, à tort ou à raison, trois contributions majeures au géomètre de Chio, lesquelles esquissent les principales articulations à venir de la géométrie grecque :
- Il aurait été le premier à rédiger des Éléments de géométrie.
- Il aurait introduit la procédure de réduction d’un problème — en l’occurrence celui de la duplication du cube — à un autre, celui de l’insertion de deux moyennes proportionnelles entre deux segments de droite (problème paradigmatique de la géométrie dite ultérieurement « solide »).
- Enfin son nom est attaché à la quadrature de certaines portions de cercle (appelées « lunules »), possiblement mobilisées pour une tentative de résolution du célébrissime problème de la quadrature du cercle.
Cette contribution nous est connue grâce à un précieux témoignage d’Eudème de Rhodes (IVe s. avant notre ère) — historien de la géométrie et disciple d’Aristote — transmis par le commentateur Simplicius (VIe s.). On y rencontre un style géométrique localement déductif, utilisant des diagrammes, déjà assez proche de celui que l’on trouvera chez Euclide.
La conservation de ce témoignage ne relève par du pur hasard : le Maître (i.e. Aristote) avait parlé d’Hippocrate et sa tentative de quadrature fut tôt interprétée comme un paralogisme. Le premier géomètre grec tant soit peu connu de nous était-il un filou ?
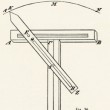
Mesurer les surfaces avec des instruments, pour lycéens (terminales), étudiants, enseignants et tout public curieux. Marie-José Durand-Richard présentera les instruments graphiques d’intégration utilisés en Europe au XIXe siècle en s’appuyant sur des documents réalisés à l’occasion de l’exposition du CNAM « Venez prendre l’aire! ».
A mi-chemin entre "Le compte est bon" et le "Trivial Poursuit", Mathador est un des rares jeux de société de mathématiques. Derrière cette invention plusieurs fois primée se cache Eric Trouillot, un professeur de collège qui rêvait de mathématiques amusantes et efficaces. Après plusieurs années de travail, c'est chose faite...
Le thème de ce numéro « Mesurer le Ciel et la Terre » invite d'emblée à situer la pratique de la mesure dans des questions de lieux : le repérage d'un lieu ou l'évaluation de distances entre lieux. Effectivement, les six articles de ce numéro correspondent à des pratiques de mesure de lieux. L'article d'AxelIe Chassagnette s'intéresse au De dimensione terrae de Caspar Peucer de 1550, aux enjeux et aux méthodes d'un calcul de la distance entre deux lieux terrestres...
La vie d’un homme savant et studieux est ordinairement étrangère au monde, et n’offre pas des incidens piquans par leur variété. Il est rare qu’elle ait quelque influence sur les événemens dont on est le plus occupé, plus rare encore qu’elle fixe la curiosité par des actions d’éclat. Car quoique la pensée tende à élever l’âme et à perfectionner le coeur ; le goût de la retraite, qui en est la suite, couvre d’une sorte d’obscurité les actions de ceux qui s’y livrent...
Cet article évoque quelques uns des artistes et mathématiciens qui ont transformé une invention d'architecte, la perspective centrale, en une théorie mathématique révolutionnaire, la géométrie projective. Il s'agit d'une brève introduction au livre Douce Perspective. Une histoire d’art et de science de Denis Favennec en collaboration avec Emmanuel Riboulet-Deyris.