CultureMath
[1] Approximation diophantienne et réseaux
[2] Une démonstration originale de l'infinité de l'ensemble des nombres premiers
[3] Sur l'algorithme RSA
[4] Arithmétique
[5] Fermat revisité
[6] Le problème des nombres gelés de Saint-Exupéry
[7] Les mathématiques du mouvement Introduction informelle aux systèmes dynamiques
[8] Petits pièges de la simulation numérique
[9] Le théorème de Sharkovskii
[10] Arbres et dérivée d'une fonction composée
[11] Homographies et suites récurrentes
[12] L'intégration selon Riemann et selon Lebesgue
[13] Signal numérique et théorie de l'échantillonnage
[14] Les intégrales de Coxeter
[15] Equirépartition d'une suite de nombres
[16] Addendum sur l'équirépartition
[17] Racine carrée fonctionnelle
[18] Le lemme de Baire
[19] Le théorème de JUEL et la surface de CLEBSCH
[20] Critères d'Ermakov
[21] Le produit d'Hadamard de deux séries entières
[22] Racine carrée fonctionnelle
[23] Jauge d'une cuve à Mazout
[24] Sur les nombres constructibles
[23] Construction des polygones réguliers
[26] Courbure des surfaces triangulées
[27] Le problème des 5 cercles
[28] Reconnaître effectivement les Ensembles Algébriques Réels
[29] Pour nouer, il faut courber
[30] Autour des triangles inscrits sur une hyperbole équilatère
[31] Gaspard Monge, de la planche `a dessin aux lignes de courbure
[32] Loi de groupe dans un triangle
[33] Les épi ou hypo trochoïdes
[34] Géométrie sur une Strophoïde
[35] Fermeture Hexagonale
[36] Cubiques circulaires passant par leurs foyers singuliers
[37] Combien de fois faut-il battre un jeu de cartes ?
[38] Avant le référendum
[39] La percolation
[40] Processus de branchement et descendance d'un individu
[41] Marches aléatoires sur Z
[42] Le jeu de Pile ou Face
[43] Le Berlekamp's switching game
[44] Jeux sur les graphes et théorème de Ramsey
[45] Jeux et stratégies
[46] Equations algébriques
[47] Intégration de polynômes, points de Gauss
[48] Les tonalités musicales vues par un mathématicien
[49] Loi de groupe sur une surface
[50] La transformation du Boulanger
[51] Rubik’s cube, groupe de poche
[52] Compte de rebonds
[53] La toupie Tippe-Top
[54] Détermination du sexe selon la température chez les crocodiles
[55] Calcul Tensoriel. Application à la relativité.
[56] Equations de Maxwell et formes différentielles, vers la relativité restreinte
[57] Les motifs des pelages d’animaux
[58] Les cercles de Tücker
[59] Interactions entre espèces, modèle de Lotka-Volterra
[60] Équation de la chaleur : traitement numérique
[61] Simulation numérique de l'équation de la chaleur
[62] Du bruit dans les images
[63] Image and movie denoising by nonlocal means
[64] Construction des entiers naturels
[65] Les axiomes de Zermelo-Fraenkel
[66] Entiers relatifs
[67] Nombres rationnels
[68] Nombres réels
[69] Nombres complexes
[70] Quaternions
[71] Ordinaux
[72] La construction des Réels par les coupures de Dedekind
[73] Laplace, Turing et la géométrie impossible du "jeu de l'imitation"
[74] La divination sikidy à Madagascar
[75] Les généralisations de la notion mathématique d'intégrale au 19e siècle
[76] Le processus d'abstraction dans le développement des premières théories de la mesure
[77] Les deux premiers journaux mathématiques français: les Annales de Gergonne (1810-1832) et le Journal de Liouville (1836-1845)
[78] Pourquoi, pour qui enseigner les mathématiques? Une mise en perspective historique des finalités et des contenus de l'enseignement des mathématiques dans la société française au XXe siècle.
[79] Les matrices : formes de représentation et pratiques opératoires (1850-1930)
[80] La loi des grands nombres, le théorème de De Moivre-Laplace
[81] La formule de Stirling
[82] Urnes aléatoires, populations en équilibre et séries génératrices
[83] Zeta de 3 est irrationnel
[84] Généalogie de populations : le coalescent de Kingman
[85] Cantor et la France
[86] Introduction à la Théorie des Groupes
[87] À la recherche de la genèse du dernier mémoire mathématique de Georg Cantor
[88] Le triangle: philosophie, histoire, mathématiques
[89] Au menu: de la géométrie à toutes les sauces
[90] Gaston DARBOUX : « Principes de Géométrie Analytique »
[91] "Souvenirs sur Sofia Kovalevskaya" de Michèle Audin
[92] Eléments d'analyse et d'algèbre (et de théorie des nombres)
[93] Pourquoi les mathématiques sont-elles difficiles ?
[94] Souvenirs sur Sofia Kovalevskaya - interview/discussion avec Michèle Audin
[96] Analyse mathématique - La maîtrise de l'implicite
[97] Epistémologie mathématique
[98] Galois, le mathématicien maudit
[99] Les Clefs pour la PSI et la PSI*
[100] Blagues mathématiques et autres curiosités
[101] Escapades arithmétiques
[102] Le jardin des courbes - Dictionnaire raisonné des courbes planes célèbres et remarquables
[101] Le problème de l'espace. Sophus Lie, Friedrich Engel et le problème de Riemann-Helmholtz
[102] Riemann : Le géomètre de la nature
[103] Eléments d'analyse et d'algèbre (et de théorie des nombres) (présentation par l’auteur)
[104] La construction tractionnelle des équations différentielles
[105] Géométrie analytique classique
[106] La passeggiata - Battements d'ailes au jardin du Luxembourg
[107] Vers une nouvelle philosophie de la nature
[108] Probabilités et statistiques aujourd'hui
[109] Des Mathématiciens de A à Z
[110] Souvenirs sur Sofia Kovalevskaya (parutions)
[111] Cantor et la France
[112] Dimensions
[113] Arithmétique
[114] La correspondance entre Henri Poincaré et les physiciens, chimistes et ingénieurs
[115] Premiers cours de philosophie positive
[116] Une Introduction à la théorie des nombres
[117] Outils mathématiques à l’usage des scientifiques et ingénieurs
[118] Nombres : Eléments de mathématiques pour philosophes
[119] Images des Mathématiques 2004-2006
[120] Leçons de mathématiques d'aujourd'hui
[121] Zoom sur les métiers des mathématiques
[122] Autour du centenaire Lebesgue
[123] L'épistémologie : état des lieux et positions
[124] Philosophie naturelle et géométrie au XVIIe siècle
[125] Les Mathématiques dans la Cité
[126] Réduction des endomorphismes
[127] Les femmes et l'enseignement scientifique
[128] Exercices de mathématiques pour physiciens
[129] La Relativité de Poincaré de 1905
[130] L'espace physique entre mathématiques et philosophie
[131] Jacques Hadamard, un mathématicien universel
[131] Un mathématicien d'exception
[132] Nouvelle bibliographie cournotienne
[133] Paul Painlevé (1863-1933). Un savant en politique
[134] La naissance de la théorie de l'information ou la force d'une idée simple
Les sondages d'opinions sont devenus partie intégrante de notre quotidien. Tout le monde sait comment ils sont effectués, dans les grandes ligne. Mais que signifient-ils exactement ? Quel crédit leur apporter ?
En nous basant sur cet exemple fondamental, nous introduisons dans ce texte la notion d'inférence statistique, en essayant de la décortiquer au maximum. Notre but est en l'occurrence de définir ce que peut-être une marge d'erreur, un intervalle de confiance.
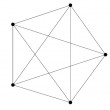
À quelle condition peut-on dessiner un graphe dans le plan, sans que ne se croisent des arêtes dudit graphe ? Le problème est assez classique : on connaît des condition nécessaires, qui dérivent de la formule d'Euler. Nous introduisons ici ces résultats, en montrant quelques applications sur des graphes particuliers.
Nous allons nous intéresser ici au nombre de manières de ranger des boules dans des boîtes. Problème classique s'il en est : nombre d'arrangements, nombre de combinaisons... Contrairement aux apparences, ce problème n'est pas toujours si simple lorsque l'on s'impose comme ici une contrainte supplémentaire : les boîtes sont indistinguables les unes des autres. Là, les choses se compliquent !
Les processus de branchement sont des modèles introduits pour étudier le développement d'une population, dans laquelle les individus se reproduisent indépendamment les uns des autres, et selon la même loi de probabilité. Introduit au 19ème siècle pour étudier la probabilité d'extinction de noms de familles illustres en Grande Bretagne, le modèle de Galton-Watson et ses variantes trouve de nombreuses applications en biologie ou en physique nucléaire.
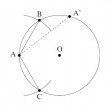
Parmi les problèmes les plus célèbres en mathématiques, la construction des polygones réguliers à la règle et au compas possède une place de choix puisqu'elle a tenu en haleine les mathématiciens pendant plus de vingt siècles. Il a fallut attendre les travaux du mathématicien allemand Gauss pour que la question soit entièrement résolue.
Reste encore un pas à franchir dans nos extensions d'ensembles de nombres. Certaines équations algébriques extrêmement simples, à coefficients réels, restent sans solution réelle (par exemple, les réels négatifs ne sont pas les carrés de réels). D'où la nécessité d'étendre encore une fois notre ensemble de nombres, en formant un sur-corps du corps des réels, dont les éléments seront appelés nombres complexes. Ce sur-corps se révélera algébriquement clos, c'est-à-dire que cette fois toute équation algébrique (à coefficients complexes) aura des solutions (complexes).
Lorsque l'on bat un jeu de cartes, selon le procédé classique qui consiste à couper le paquet en deux parties puis à alterner les cartes des deux parties pour reformer un seul tas (puis à recommencer l'opération un certain nombre de fois), le but est bien sûr qu'aucun joueur ne puisse deviner l'ordre des cartes après battage. Manifestement, si l'on ne bat qu'une seule fois, un joueur attentif qui connaissait l'ordre initial des cartes dispose encore de certaines informations. D'où la question de savoir combien de fois il faut battre le paquet de cartes pour qu'il soit "bien mélangé".
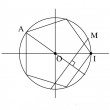
Si l'on trace les cercles circonscrits aux cinq triangles correspondant aux "branches" d'une étoile à cinq branches, on s'aperçoit que les points d'intersection de chacun de ces cercles avec le suivant sont cocycliques !
Ce problème de géométrie assez classique à été remis au goût du jour par le président chinois, à l'occasion du congrès international des mathématiciens (Pékin, août 2002).
Étant donné un cercle, si l'on trace une corde au hasard sur ce cercle, quelle est la probabilité pour que celle-ci soit plus longue que le rayon du cercle ? Cette question, connue sous le nom de "paradoxe" de la corde de Bertrand, est particulièrement judicieuse pour illustrer la notion de mesure de probabilité. Nous allons voir que la réponse varie en fonction du mode de construction, chaque façon de penser étant lié à une mesure particulière.
On connaît des formules de dérivation à un ordre quelconque pour un produit de fonction (formule de Leibnitz). Pour ce qui est d'une somme de fonctions, c'est encore plus évident : la dérivée n-ième de la somme est la somme des dérivées n-ièmes, par linéarité. En revanche, pour ce qui est de la composée de deux fonctions, on ne sais pas faire... Nous allons voir ici que le problème se transpose en quelque chose de purement combinatoire sur les arbres.