CultureMath
Lorsque l'on bat un jeu de cartes, selon le procédé classique qui consiste à couper le paquet en deux parties puis à alterner les cartes des deux parties pour reformer un seul tas (puis à recommencer l'opération un certain nombre de fois), le but est bien sûr qu'aucun joueur ne puisse deviner l'ordre des cartes après battage. Manifestement, si l'on ne bat qu'une seule fois, un joueur attentif qui connaissait l'ordre initial des cartes dispose encore de certaines informations. D'où la question de savoir combien de fois il faut battre le paquet de cartes pour qu'il soit "bien mélangé".
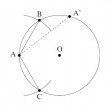
Étant donné un cercle, si l'on trace une corde au hasard sur ce cercle, quelle est la probabilité pour que celle-ci soit plus longue que le rayon du cercle ? Cette question, connue sous le nom de "paradoxe" de la corde de Bertrand, est particulièrement judicieuse pour illustrer la notion de mesure de probabilité. Nous allons voir que la réponse varie en fonction du mode de construction, chaque façon de penser étant lié à une mesure particulière.