CultureMath
Ressources adaptées au programme de mathématiques de terminale S
Le programme des premières S (B.O. 2011) est disponible en version pdf.
Il est découpé en trois grands thèmes (plus deux pour l'enseignement de spécialité), et assorti de deux capacités transversales. Cliquez sur les différents thèmes pour obtenir une liste de ressources CultureMATH correspondantes.
- Analyse
- Géométrie
- Statistique et probabilités
- Arithmétique (enseignement de spécialité)
- Matrices et suites (enseignement de spécialité)
Deux capacités transversales :
Ce texte part d'une observation expérimentale: quand on calcule une trentaine ou plus de valeurs de 2n , on constate que le premier chiffre est nettement plus souvent "1" que n'importe quel autre. Il arrive dans plus de 30% des cas ! Mais que signifie ce pourcentage ?
Ce texte nous donne quelques exemples de singularités lagrangiennes. Mais ne vous effrayez pas tout de suite ! L'auteur prend le parti de ne jamais définir cette notion, préférant tourner autour en prenant plusieurs points de vue amusants (ceux qui donnent son titre à l'exposé) pour insuffler l'intuition de ce qu'elles sont.
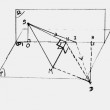
Le principe de Femat s'énonce de manière simple : Pour aller d'un point-source S à un point-détecteur D après une réflexion ou une réfraction, la lumière suit un chemin pour lequel le temps de parcours est extrêmal (i.e. minimal ou maximal). A partir de ce principe, ce texte démontre les lois classiques de la réflexion et de la réfraction (en particulier la Loi de Descartes).
Né en 1973 à Paris, Fabien Napolitano est directeur général du site Brestois de la société Ixsea, leader mondial dans le domaine des systèmes de positionnement pour les bateaux et sous-marins. Pourtant il n'a pas fait d'études d'ingénierie, mais est titulaire d'un doctorat en mathématiques pures, et a fait des aller-retours entre le monde de la recherche fondamentale et celui de l'industrie.
Le "petit théorème de Fermat" est un bijou de simplicité et d'utilité. Depuis sa découverte il y a plus de 400 ans par Fermat, on l'a redémontré d'au moins 100 manières différentes ! Dans ce texte, à la limite des programmes d'arithmétique de terminale scientifique, nous vous proposons de (re)découvrir ce petit joyau sous plusieurs points de vue, ainsi que des applications (Wilson) et des réciproques partielles.
L'expérience du dessin de plans et la curiosité scientifique de Gaspard Monge ont à notre avis influencé sa manière, très visuelle, de raisonner en mathématiques. Il était aussi un enseignant remarquable. Le souci de former les futurs cadres de la nation, donc d'expliquer à la fois les notions mathématiques et leurs éventuelles applications est sans doute lié à son besoin de voir et de représenter de manière précise les objets mathématiques qu'il définit.
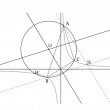
Ce texte a une forme inhabituelle sur ce site : c'est un problème destiné à explorer certaines propriétés de l'hyperbole y = 1/x. Il mélange géométrie plane, géométrie analytique et utilisation des moyens de calcul modernes, et pourra donner des idées d'exercices aux professeurs... tout en leur pemettant de s'exercer !
C. F. Gauss est toujours considéré par certains comme le plus grand mathématicien de tous les temps. Sa capacité calculatoire hors du commun, couplée à son goût pour la contemplation des idées abstraites l'on amené à résoudre des problèmes (parfois vieux de millénaires !) et à envisager avec une clarté géniale (bien qu'inquiète) les idées qui feraient les mathématiques du futur.
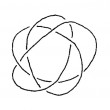
Quand on découvre les mathématiques, on étudie des formes et des nombres. Une manière usuelle d'associer des nombres à une forme est de mesurer des longueurs. Ce texte nous présente de façon intuitive les notions de courbure et de torsion des courbes et des surfaces, et présente un théorème classique sur la courbure des nœuds...
Dans un article de 1950, devenu justement célèbre, Alan Turing propose, en vue d'opérer une comparaison fonctionnelle entre le cerveau et la machine, un jeu qu'il appelle "jeu de l'imitation". Cet article fut un pas décisif dans le domaine de la philosophie de la connaissance.
Le texte que nous vous proposons présente un point de vue cognitif sur la question de la différence entre la pensée humaine, continue, et le fonctionnement d'une machine à états discrets.