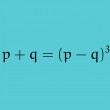CultureMath
Auteur : Maxime Bourrigan, École Normale Supérieure
Mots-clefs : Arithmétique, Algorithme, PGCD
Le but de ce document est d'introduire les propriétés les plus élémentaires du PGCD et de l'algorithme d'Euclide, tout d'abord de façon très directe, puis en abordant dans un second temps les propriétés liées au théorème de Bézout. Dans une partie intermédiaire, on propose une implémentation de l'algorithme d'Euclide à l'aide du logiciel Algobox.
Question du jeudi #32 : Montrer que le nombre $R_n = \underbrace{111\ldots 111}_{n\ \text{chiffres}}$ n'est pas un carré si $n > 1$.
Question du jeudi #27 : Le plus grand nombre premier connu à ce jour est 257 885 161 - 1. Quels sont ses deux derniers chiffres ?
Question du jeudi #26 : Déterminer les couples $(p, q)$ de nombres premiers tels que $p + q = (p-q)^3$.
Question du jeudi #19 : On dit qu'un entier $n$ est une anagramme de $m$ si on peut écrire $n$ en permutant les chiffres de $m$. On ne compte pas les 0 non significatifs que l'on peut ajouter à gauche : 330 est une anagramme de 303, mais pas de (0)33.
Une puissance de 2 peut-elle être l'anagramme d'une autre puissance de 2 ?
Question du jeudi #16 : Les nombres de Fibonacci $(F_n)_{n\in\mathbb N}$ sont définis par $F_0 = 0$, $F_1 = 1$ et la relation de récurrence $F_{n+1} = F_n + F_{n-1}$. Montrer qu'il existe $n > 0$ tel que $F_n$ se termine par 2015 zéros.
Question du jeudi #9 : Montrer que, parmi dix-huit nombres à trois chiffres consécutifs, il en existe toujours un qui soit un multiple de la somme de ses chiffres.
Question du jeudi #2 : Les six derniers chiffres d'une puissance de 2 sont tous des 6 et des 9. Pouvez-vous les déterminer exactement ?
Un des exercices du Google Code Jam de 2008 demandait de calculer les trois derniers chiffres avant la virgule du nombre $(3+\surd 5)^n$. On explique ici comment calculer ces chiffres presque instantanément en exploitant une jolie propriété arithmétique de $3+\surd 5$.