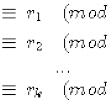CultureMath
Dans ce chapitre nous avons sélectionné deux types de sources. D’une part, des énoncés choisis pour leur présentation imagée du problème : sous un habillage « concret », ces textes nous montrent entre autres l’imagination au service des mathématiques. C’est ce qui a motivé leur regroupement et non les mathématiques mises en œuvre pour la résolution. Certaines solutions sont « brutes », d’autres sont accompagnées de commentaires, d’explications, ou de véritable justification mathématique.
Nous étudions, dans ce chapitre, la résolution d’un système de deux congruences simultanées, les modules étant premiers entre eux, telle qu’elle serait menée au lycée. Même si nous nous appuyons sur un problème historique, nous employons les notations modernes, notamment le signe de congruence introduit par Gauss...
Voici une séquence de travail scénarisée autour d’un texte proposant un algorithme qui permet de résoudre un système de trois congruences simultanées modulo des entiers premiers entre eux deux à deux.
Le problème dit des restes chinois apparaît d’abord en Chine entre le 3e et le 5e siècle de notre ère dans le Classique mathématique de Maître Sun, préoccupe le mathématicien indien Bhaskara au 7e siècle, refait surface au Moyen-Orient au 10e siècle et en Chine au 13e siècle, et devient commun en Europe à partir du 13e siècle. Il est complètement résolu par Leonhard Euler au 18e siècle, avant de devenir le b-a-ba de la nouvelle arithmétique des congruences que nous devons au génie de Carl Friedrich Gauss (1777-1855).
Le théorème des restes chinois. Textes, commentaires et activités pour l’arithmétique au lycée
Les problèmes de congruences simultanées sont connus dans l'histoire des mathématiques comme « problèmes des restes » ou « des restes chinois ». C'est un sujet qui a donné lieu, depuis des siècles, à de riches développements mathématiques et dont l'origine reste hypothétique puisqu'il est très difficile de démêler les motivations premières qui en ont suscité l’intérêt ...
La fonction zêta de Riemann, définie par $\displaystyle{\zeta ( s) = \sum_{ n=1}^{ + \infty} \frac{ 1}{ n^s}}$ (pour ${Re}~ s > 1$), intéresse les mathématiciens depuis longtemps, et elle est encore à l'heure actuelle très étudiée, car cette fonction est fortement liée aux propriétés des nombres premiers. Dans ce texte issu d'un Mémoire de M1, nous étudions quelques propriétés arithmétiques et algébriques des valeurs de $\zeta (s)$ aux points entiers $s \in \mathbb{N}$, $s \geqslant 2$, telles que l'irrationalité ou la transcendance. Notamment, nous fournissons une démonstration complète et élémentaire, due à Beukers, du théorème d'Apéry (1978) selon lequel $\zeta(3)$ est irrationnel; cette démonstration est tout à fait accessible à un étudiant de Licence ou de classes préparatoires.
This article features a new type of algorithm whose goal is to give a better understanding of how prime numbers form themselves. It is called the Prime-Generating Algorithm or PGA.